Program
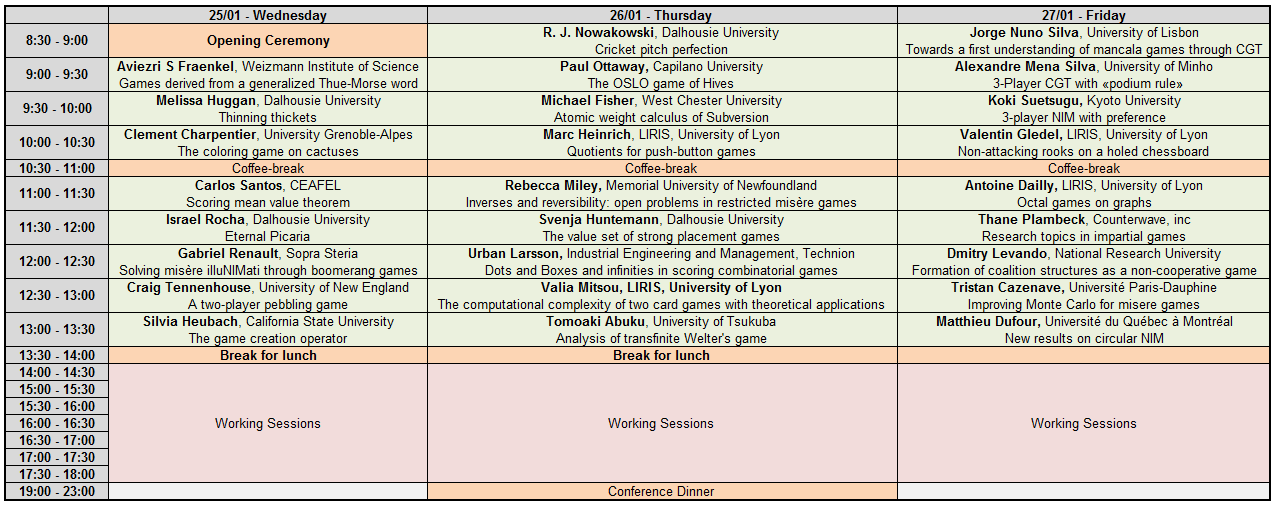
Standard Talks, Mornings (8:00-13:00) - Building C6, Room 6.2.56
Working Sessions, Afternoons (14:00-18:00) - Building C8, Rooms 8.2.11, 8.2.13, 8.2.17, 8.2.19
Aviezri S. Fraenkel, Weizmann Institute of Science
Title: Games derived from a generalized Thue-Morse word
Abstract: It is always nice to make connections between different areas of mathematics. For fusing combinatorial game theory with combinatorics on words, we begin with some brief relevant background on words and automata theory, followed by devising and analyzing a triple of games derived from a generalization of the Thue-Morse word.
(Joint work with Michel Rigo.)
(Joint work with Michel Rigo.)
Melissa Huggan, Dalhousie University
Title: Thinning Thickets
Abstract: The game of Thinning Thickets is played on a directed graph and can be regarded as an offshoot of Hackenbush. Throughout this talk, we will present results for Thinning Thickets on very thin trees, cordons, which are stalks with at most one leaf at each vertex. In particular, we prove that Thinning Thickets has infinite boiling point. We also show that the nim-dimension for Green Cordons is infinite and characterize those with nim-value 0 and nim-value 1. We give a characterization for nim-value 2 and for 3 if the cordons have two or fewer leaves. For multi-colored stalks, we show that, up to infinitesimals, these take on only eight values.
(joint work with Richard Nowakowski)
Clement Charpentier, University Grenoble-Alpes
(joint work with Urban Larsson)
Gabriel Renault, Sopra Steria
Title: Solving misère illuNIMati through boomerang games
Abstract: IlluNIMati is a partizan variant of NIM in which tokens are triangles with a blue vertex, a green vertex and a red vertex. Only Left may play in a heap where the vertex facing North of the top triangle is blue. Only Right may play in a heap where the vertex facing North of the top triangle is red. They may both play in a heap where the vertex facing North of the top triangle is green. However, after removing any positive number of triangles of a heap, they may turn this heap, choosing which vertex faces North. We consider illuNIMati positions within a bigger set of games, called boomerang games, to solve the misère version.
Craig Tennenhouse, University of New England
Title: A two-player pebbling game
Abstract: Blocking Pebbles is a partizan game based on graph pebbling directed acyclic graphs. We demonstrate some results on oriented trees, and find numbers, nimbers, and some infinitesimals on the out-star.
(joint work with Mike Fisher)
Silvia Heubach, California State University
R. J. Nowakowski, Dalhousie University
Title: Cricket pitch perfection
Abstract: A cricket Pitch is a path with bumps (non-negative weights) and a roller that resides at the vertices. Left rolls (one or more edges) to the left and Right to the right reducing each bump by 1. The roller cannot go over a 0-edge, this part is `perfect'. Nowakowski and Ottaway partially solved the game. Nowakowski and (Angela) Siegel give a complete solution in terms of reductions and ordinal sums.
(joint work with Paul Ottaway and Angela Siegel)
Paul Ottaway, Capilano University
Title: The OSLO game of Hives
Abstract: Hives is a one-sided loopy (OSLO) game played on a graph with white and red vertices. On Right's turn, they may colour any white vertex red as long as the set of red vertices form an independent set. On Left's turn, they may swap the colour of any two adjacent vertices as long as the red vertices remain an independent set. Note that Left has the equivalent of a pass move by selecting a pair of adjacent white vertices while Right does not have a pass move. The game ends when the red vertices form a maximal independent set. In this talk, we will examine the game values and algebraic structure that exists in Hives, provide strategies for certain classes of graphs as well as decomposition theorems for general graphs.
Michael Fisher, West Chester University
Title: Atomic weight calculus of Subversion
Abstract: In this work we analyze Subversion, a recently proposed all-small combinatorial ruleset. Often, the atomic weight calculus, allowing the recursive computation of the atomic weight of a game G with the atomic weights of its options, is not easy. However, Subversion is an interesting case such that the theoretical difficult cases are reduced to a finite number of cases and organized in a table. With the table, given a Subversion position (a,b), a≥b, using the Euclidean algorithm and the continued fraction representation of a/b, it is possible to compute aw(a,b). An algorithm for that is presented.
(joint work with Neil McKay, Richard J. Nowakowski, Paul Ottaway and Carlos Santos)
Marc Heinrich, LIRIS, University of Lyon
Title: Quotients for push-button games
Abstract: We study a new construction which aims at solving the following question: what happens if we allow players to change the rules of the game during the play? Given two rulesets R0 and R1, we create a new ruleset R0 ⇒ R1 corresponding to the following: the two players play according to rules R0 until one of the players at its turn pushes an imaginary button, changing the rules to R1. We study how several classical impartial games like Nim, Wythoff, Euclid or Cram combine with this construction. By adapting indistinguishably quotients (technique of Plambeck, 2005), we look at how these new rules behave for sums of positions. We show that it is possible to give values to game positions which behave similarly to Grundy values.
(joint work with Eric Duchêne, Urban Larsson, Aline Parreau)
Rebecca Miley, Memorial University of Newfoundland
Title: Inverses and reversibility: open problems in restricted misère games
Abstract: Much progress has been made in misère game theory using the technique of "restricted" misère play, where games can be considered equivalent inside a restricted set of games without being equal in general. Restricted misère play exhibits much more structure than general misère play, but there are a number of curious properties that complicate matters: (1) a position can have an additive inverse that is not its negative, and (2) a position can satisfy reversibility through an end (a game with Left but not Right options, or vice versa). These properties do not occur in normal play and general misère play, respectively. This talk presents a survey of recent developments in restricted misère games and discusses open problems related to invertibility and reversibility.
(Based on joint work with Gabriel Renault)
Svenja Huntemann, Dalhousie University
Title: The value set of strong placement games
Abstract: We are interested in what values strong placement games, a class of games including Domineering and Snort, can take under normal play. In studying this question, we take advantage of the one-to-one correspondence between strong placement games and simplicial complexes (with vertex set bipartitioned), and the known structure of the game tree. Among others, we will show that all numbers are possible.
Urban Larsson, Industrial Engineering and Management, Technion
Title: Dots and Boxes and infinities in scoring combinatorial games
Abstract: We study an extension of the Guaranteed scoring universe (presented at CGTC I), where infinities are used (as threats) to terminate a game. A new reduction is obtained, and we use it to find the simplest form for a basic Dots and Boxes position, namely an open ended double box.
(joint work with Richard Nowakowski and Carlos Pereira dos Santos)
Valia Mitsou, LIRIS, University of Lyon
Title: The computational complexity of two card games with theoretical applications
Abstract: The main theme of this talk is card games that can be naturally reformulated as well-known graph-theoretic games. In particular, we will focus on two different card games: the game of SET and the game of UNO. The objective of the former is to form sets of cards that match in a certain sense, while in the latter the players need to discard their cards following a matching rule (for more details regarding the rules of the two games please visit the following websites: official website of SET, wikihow: how to play UNO). We show natural reformulations of SET as arc-kayles and of UNO as generalized geography and present some complexity results about them.
Tomoaki Abuku, University of Tsukuba
Title: Analysis of transfinite Welter's game
Abstract: As well-known, in impartial game, we can judge which player can win in a position of game by its Grundy number. Deciding Grundy numbers in Welter's Game is fairly complicated even in its original form. In this talk, we analyze the transfinite version of Welter's Game, namely its extension into the set of general ordinal numbers.
Jorge Nuno Silva, University of Lisbon; Alex de Voogt, AMNH, New York
Title: Towards a first understanding of mancala games through CGT
Abstract: Only few traditional games have been analyzed using combinatorial game theory (CGT), specifically Konane and Tiouk-Tiouk. The class of mancala games shows at least one example of another traditional game to which CGT can be applied. We explored the variant Hawalis, currently played competitively in Oman. The values of the studied end-game positions give insight in the game. This approach looks promising to this variant and potentially other variants of the mancala family.
Alexandre Mena Silva, University of Minho
Title: 3-Player CGT with «podium rule»
Abstract: In the first part of the talk, we briefly discuss the state of art about the research on combinatorial 3-player games. Playing with the «podium rule convention», if a player cannot be last, he tries to be last but one. In his paper «N-person Nim and N-person Moore's games», S Liu presented a very elegant characterization of the P-positions of 3-player NIM with podium rule (and, in general, for N-player NIM). In the second part of the talk, we show how Liu’s work can be extended, presenting the general reduction process and related canonical forms.
(joint work with Richard J. Nowakowski and Carlos Santos)
Koki Suetsugu, Kyoto University
Title: 3-player NIM with preference
Abstract: In order to analyze multiplayer CGT, we need to consider the objectives of players that are guaranteed to lose. For example, in a 3-player game where one player cannot win, it is still possible that she can determine whether the next player or previous player will win. In this presentation, we assume each player has a fixed “preference”, which is defined as a total ordering of the other players, and each player’s preference is known by all other players. When a player cannot win, she behaves so that the winner will have the highest possible preference value. We present solutions for various forms of preferences in 3-player NIM.
Title: Non-attacking rooks on a holed chessboard
Abstract: In this game, inspired by the Non-Attacking Queens Game (Noon and Van Brummelen, 2006), two players alternately put rooks on a chessboard with the restriction that no rook should be able to capture another one. The last player to play wins. If the chessboard is a rectangular grid, the problem reduces to a parity game. In this work we consider the case where there is a hole in the chessboard. This problem is much more difficult and leads to the introduction of a game played on graphs that can be sees as a generalization of Arc-Kayles. We solved this latter game for simple graphs and found some general properties.
(joint work with Nicolas Bousquet, Antoine Dailly and Marc Heinrich)
Title: Octal games on graphs
Abstract: Octal games are a well-defined family of two-player games played on heaps of counters, in which the two players take turns removing a certain number of counters from a heap, sometimes being allowed to split a heap in two nonempty heaps, until no counters can be removed anymore. We extend the definition of octal games to play them on graphs: heaps are replaced by connected components and counters by vertices. Thus, an octal game on a path of n vertices is equivalent to playing the same octal game on a heap of n counters. We study one of the simplest octal games, called 0.33, in which the players can remove one vertex or two adjacent vertices without disconnecting the graph, on trees. We present a thorough study of the game on subdivided stars and bistars.
Thane Plambeck, Counterwave, inc
Title: Research topics in Impartial Games
Abstract: A selection of fundamental problems in Impartial games that still bug me and that I wish people would work on.
Dmitry Levandu, National Research University
Title: Formation of coalition structures as a non-cooperative game
Abstract: The paper defines a non-cooperative simultaneous finite game with an arbitrary fixed number of potential deviators. A definition of the game embeds a coalition formation mechanism, which includes a number of deviators, a set of eligible partitions and coalition formation rule. The game has an equilibrium in mixed strategies. The equilibrium encompasses intra and inter group externalities and an individual payoff allocation that make it different from a strong Nash, coalition-proof equilibrium and certain other equilibrium concepts. We offer a non- cooperative stability criterion to describe the robustness of an equilibrium strategy profile with respect to an to an increase in the number of deviators. The criterion may serve to measure self-enforcement property of an equilibrium and focal points of a game.
Tristan Cazenave, Université Paris-Dauphine
Title: Improving Monte Carlo for misere games
Abstract: Monte Carlo Tree Search with random playouts can be much improved in misere games by avoiding losing moves in playouts. We will show on multiple misere games that this simple modification can improve drastically the level of play. We will also consider the combination with playout policy learning.
Matthieu Dufour, Université du Québec à Montréal
Title: New results on circular NIM
Abstract: Matthieu Dufour and Silvia Heubach have been studying Circular Nim, a variation on the well-known game of NIM. This t:wo player game, described with two parameters and noted C(n,k), is played in the following way: n stacks of tokens are arranged in a circular way, and a move consists of choosing k consecutive stacks of this circular arrangement and then taking at least one token from one or more of the k stacks. In normal play, C(n,1), C(n,n-1) and C(n,n) are trivial. C(4,2) is easy, C(5,2), C(5,3) and C(6,3) are known since (Ehrenborg and, Steingrimsson, 1996) and C(6,4) and C(8,6) were solved by Dufour and Heubach (2012). We will present some more results, conjectures and comments on the misere play of that game.

(joint work with Richard Nowakowski)
Clement Charpentier, University Grenoble-Alpes
Title: The coloring game on cactuses
Abstract: The coloring game on a graph G is a game where the two players, Alice and Bob, are taking turns coloring a yet-uncolored vertex of G with a color chosen into a set C. Alice wins if the manage to color G entirely and Bob wins if a vertex in uncolorable at some point. We denote by Xg(G) the smallest number of colors for which Alice has a winning strategy. A graph is (1,k)-decomposable if its edges can be partitionned into two subsets, one inducing a forest and the other inducing a subgraph of maximum degree at most k. For any forest F, χg(F)≤4 (Faigle et al, 1993). We know, thanks to He et al. (2002), that χg(G)≤4+k for any (1,k)-decomposable graph. Montassier et al. (2012) proved that any planar graph of girth at least 8 is (1,1)-decomposable, and so χg(G)≤5. We prove this bound is best possible, even for graphs with arbitrary large girth and for several subclasses of planar graphs, by a result on cactuses. A cactus is a graph whose edges all belong to at most one cycle (which makes them all planars).
Theorem: For every integer g≥3, d≥0, there is a cactus C of girth g with distance between cycles at least d and for which χg(C)=5.
Carlos Pereira dos Santos, CEAFEL, University of Lisbon
n.m(G)-t ≤ n.G ≤ n.m(G)+t (for some fixed perturbation t).
In this work, we discuss the occurrence of a mean value in the guaranteed scoring universe which is, in some sense, two-dimensional due the different nature of moves and points.
(joint work with Richard Nowakowski and Urban Larsson)Theorem: For every integer g≥3, d≥0, there is a cactus C of girth g with distance between cycles at least d and for which χg(C)=5.
Carlos Pereira dos Santos, CEAFEL, University of Lisbon
Title: Scoring mean value theorem
Abstract: Regarding short Conway’s group, a value of a game can be thought of as an indeterminate cloud, covering the confusion interval. In such a situation it is natural to ask – Is there a fair settlement about the value of a game? The answer is well-known; it is the mean value m(G) (a number), satisfyingn.m(G)-t ≤ n.G ≤ n.m(G)+t (for some fixed perturbation t).
In this work, we discuss the occurrence of a mean value in the guaranteed scoring universe which is, in some sense, two-dimensional due the different nature of moves and points.
Israel Rocha, Dalhousie University
Title: Eternal Picaria
Abstract: Picaria is a traditional board game, played by the Zuni tribe of the American Southwest and other parts of the world, such as a rural Southwest region in Sweden. It is related to the popular children's game of Tic-tac-toe, but the 2 players have only 3 stones each, and in the second phase of the game, pieces are slided, along speci_ed move edges, in attempts to create the three-in-a-row. We provide a rigorous solution, and prove that the game is a draw; moreover our solution gives insights to strategies that players can use.(joint work with Urban Larsson)
Gabriel Renault, Sopra Steria
Title: Solving misère illuNIMati through boomerang games
Abstract: IlluNIMati is a partizan variant of NIM in which tokens are triangles with a blue vertex, a green vertex and a red vertex. Only Left may play in a heap where the vertex facing North of the top triangle is blue. Only Right may play in a heap where the vertex facing North of the top triangle is red. They may both play in a heap where the vertex facing North of the top triangle is green. However, after removing any positive number of triangles of a heap, they may turn this heap, choosing which vertex faces North. We consider illuNIMati positions within a bigger set of games, called boomerang games, to solve the misère version.
Craig Tennenhouse, University of New England
Title: A two-player pebbling game
Abstract: Blocking Pebbles is a partizan game based on graph pebbling directed acyclic graphs. We demonstrate some results on oriented trees, and find numbers, nimbers, and some infinitesimals on the out-star.
(joint work with Mike Fisher)
Silvia Heubach, California State University
Title: The game creation operator
Abstract: We investigate the properties of an operator on a specific type of combinatorial games, namely subtraction games. A subtraction game is played by two players, who alternately remove tokens from a set of stacks of tokens according to the rules specified in the move set M. This is an impartial game (both players have the same moves and there is no randomness), so one can compute the positions from which the second player can win (P-positions) the game with rule-set M. A new game M* is created by making these P-positions the moves of the new game. Re-interpreting P-positions as moves is possible because for subtraction games, the structure of positions and moves is the same. We will show that the misère star-operator converges to a limit game in any dimension and characterize the limit game via features of the original game. We will also discuss the structure of the limit games in one and two dimensions. No prior knowledge of combinatorial games is needed even though such a background is helpful.
(joint work with Matthieu Dufour and Urban Larsson)
(joint work with Matthieu Dufour and Urban Larsson)
R. J. Nowakowski, Dalhousie University
Title: Cricket pitch perfection
Abstract: A cricket Pitch is a path with bumps (non-negative weights) and a roller that resides at the vertices. Left rolls (one or more edges) to the left and Right to the right reducing each bump by 1. The roller cannot go over a 0-edge, this part is `perfect'. Nowakowski and Ottaway partially solved the game. Nowakowski and (Angela) Siegel give a complete solution in terms of reductions and ordinal sums.
(joint work with Paul Ottaway and Angela Siegel)
Paul Ottaway, Capilano University
Title: The OSLO game of Hives
Abstract: Hives is a one-sided loopy (OSLO) game played on a graph with white and red vertices. On Right's turn, they may colour any white vertex red as long as the set of red vertices form an independent set. On Left's turn, they may swap the colour of any two adjacent vertices as long as the red vertices remain an independent set. Note that Left has the equivalent of a pass move by selecting a pair of adjacent white vertices while Right does not have a pass move. The game ends when the red vertices form a maximal independent set. In this talk, we will examine the game values and algebraic structure that exists in Hives, provide strategies for certain classes of graphs as well as decomposition theorems for general graphs.
Michael Fisher, West Chester University
Title: Atomic weight calculus of Subversion
Abstract: In this work we analyze Subversion, a recently proposed all-small combinatorial ruleset. Often, the atomic weight calculus, allowing the recursive computation of the atomic weight of a game G with the atomic weights of its options, is not easy. However, Subversion is an interesting case such that the theoretical difficult cases are reduced to a finite number of cases and organized in a table. With the table, given a Subversion position (a,b), a≥b, using the Euclidean algorithm and the continued fraction representation of a/b, it is possible to compute aw(a,b). An algorithm for that is presented.
(joint work with Neil McKay, Richard J. Nowakowski, Paul Ottaway and Carlos Santos)
Marc Heinrich, LIRIS, University of Lyon
Title: Quotients for push-button games
Abstract: We study a new construction which aims at solving the following question: what happens if we allow players to change the rules of the game during the play? Given two rulesets R0 and R1, we create a new ruleset R0 ⇒ R1 corresponding to the following: the two players play according to rules R0 until one of the players at its turn pushes an imaginary button, changing the rules to R1. We study how several classical impartial games like Nim, Wythoff, Euclid or Cram combine with this construction. By adapting indistinguishably quotients (technique of Plambeck, 2005), we look at how these new rules behave for sums of positions. We show that it is possible to give values to game positions which behave similarly to Grundy values.
(joint work with Eric Duchêne, Urban Larsson, Aline Parreau)
Rebecca Miley, Memorial University of Newfoundland
Title: Inverses and reversibility: open problems in restricted misère games
Abstract: Much progress has been made in misère game theory using the technique of "restricted" misère play, where games can be considered equivalent inside a restricted set of games without being equal in general. Restricted misère play exhibits much more structure than general misère play, but there are a number of curious properties that complicate matters: (1) a position can have an additive inverse that is not its negative, and (2) a position can satisfy reversibility through an end (a game with Left but not Right options, or vice versa). These properties do not occur in normal play and general misère play, respectively. This talk presents a survey of recent developments in restricted misère games and discusses open problems related to invertibility and reversibility.
(Based on joint work with Gabriel Renault)
Svenja Huntemann, Dalhousie University
Title: The value set of strong placement games
Abstract: We are interested in what values strong placement games, a class of games including Domineering and Snort, can take under normal play. In studying this question, we take advantage of the one-to-one correspondence between strong placement games and simplicial complexes (with vertex set bipartitioned), and the known structure of the game tree. Among others, we will show that all numbers are possible.
Urban Larsson, Industrial Engineering and Management, Technion
Title: Dots and Boxes and infinities in scoring combinatorial games
Abstract: We study an extension of the Guaranteed scoring universe (presented at CGTC I), where infinities are used (as threats) to terminate a game. A new reduction is obtained, and we use it to find the simplest form for a basic Dots and Boxes position, namely an open ended double box.
(joint work with Richard Nowakowski and Carlos Pereira dos Santos)
Valia Mitsou, LIRIS, University of Lyon
Title: The computational complexity of two card games with theoretical applications
Abstract: The main theme of this talk is card games that can be naturally reformulated as well-known graph-theoretic games. In particular, we will focus on two different card games: the game of SET and the game of UNO. The objective of the former is to form sets of cards that match in a certain sense, while in the latter the players need to discard their cards following a matching rule (for more details regarding the rules of the two games please visit the following websites: official website of SET, wikihow: how to play UNO). We show natural reformulations of SET as arc-kayles and of UNO as generalized geography and present some complexity results about them.
Tomoaki Abuku, University of Tsukuba
Title: Analysis of transfinite Welter's game
Abstract: As well-known, in impartial game, we can judge which player can win in a position of game by its Grundy number. Deciding Grundy numbers in Welter's Game is fairly complicated even in its original form. In this talk, we analyze the transfinite version of Welter's Game, namely its extension into the set of general ordinal numbers.
Jorge Nuno Silva, University of Lisbon; Alex de Voogt, AMNH, New York
Title: Towards a first understanding of mancala games through CGT
Abstract: Only few traditional games have been analyzed using combinatorial game theory (CGT), specifically Konane and Tiouk-Tiouk. The class of mancala games shows at least one example of another traditional game to which CGT can be applied. We explored the variant Hawalis, currently played competitively in Oman. The values of the studied end-game positions give insight in the game. This approach looks promising to this variant and potentially other variants of the mancala family.
Alexandre Mena Silva, University of Minho
Title: 3-Player CGT with «podium rule»
Abstract: In the first part of the talk, we briefly discuss the state of art about the research on combinatorial 3-player games. Playing with the «podium rule convention», if a player cannot be last, he tries to be last but one. In his paper «N-person Nim and N-person Moore's games», S Liu presented a very elegant characterization of the P-positions of 3-player NIM with podium rule (and, in general, for N-player NIM). In the second part of the talk, we show how Liu’s work can be extended, presenting the general reduction process and related canonical forms.
(joint work with Richard J. Nowakowski and Carlos Santos)
Koki Suetsugu, Kyoto University
Title: 3-player NIM with preference
Abstract: In order to analyze multiplayer CGT, we need to consider the objectives of players that are guaranteed to lose. For example, in a 3-player game where one player cannot win, it is still possible that she can determine whether the next player or previous player will win. In this presentation, we assume each player has a fixed “preference”, which is defined as a total ordering of the other players, and each player’s preference is known by all other players. When a player cannot win, she behaves so that the winner will have the highest possible preference value. We present solutions for various forms of preferences in 3-player NIM.
Valentin Gledel, LIRIS, University of Lyon
Title: Non-attacking rooks on a holed chessboard
Abstract: In this game, inspired by the Non-Attacking Queens Game (Noon and Van Brummelen, 2006), two players alternately put rooks on a chessboard with the restriction that no rook should be able to capture another one. The last player to play wins. If the chessboard is a rectangular grid, the problem reduces to a parity game. In this work we consider the case where there is a hole in the chessboard. This problem is much more difficult and leads to the introduction of a game played on graphs that can be sees as a generalization of Arc-Kayles. We solved this latter game for simple graphs and found some general properties.
(joint work with Nicolas Bousquet, Antoine Dailly and Marc Heinrich)
Antoine Dailly, LIRIS, University of Lyon
Title: Octal games on graphs
Abstract: Octal games are a well-defined family of two-player games played on heaps of counters, in which the two players take turns removing a certain number of counters from a heap, sometimes being allowed to split a heap in two nonempty heaps, until no counters can be removed anymore. We extend the definition of octal games to play them on graphs: heaps are replaced by connected components and counters by vertices. Thus, an octal game on a path of n vertices is equivalent to playing the same octal game on a heap of n counters. We study one of the simplest octal games, called 0.33, in which the players can remove one vertex or two adjacent vertices without disconnecting the graph, on trees. We present a thorough study of the game on subdivided stars and bistars.
Thane Plambeck, Counterwave, inc
Title: Research topics in Impartial Games
Abstract: A selection of fundamental problems in Impartial games that still bug me and that I wish people would work on.
Dmitry Levandu, National Research University
Title: Formation of coalition structures as a non-cooperative game
Abstract: The paper defines a non-cooperative simultaneous finite game with an arbitrary fixed number of potential deviators. A definition of the game embeds a coalition formation mechanism, which includes a number of deviators, a set of eligible partitions and coalition formation rule. The game has an equilibrium in mixed strategies. The equilibrium encompasses intra and inter group externalities and an individual payoff allocation that make it different from a strong Nash, coalition-proof equilibrium and certain other equilibrium concepts. We offer a non- cooperative stability criterion to describe the robustness of an equilibrium strategy profile with respect to an to an increase in the number of deviators. The criterion may serve to measure self-enforcement property of an equilibrium and focal points of a game.
Tristan Cazenave, Université Paris-Dauphine
Title: Improving Monte Carlo for misere games
Abstract: Monte Carlo Tree Search with random playouts can be much improved in misere games by avoiding losing moves in playouts. We will show on multiple misere games that this simple modification can improve drastically the level of play. We will also consider the combination with playout policy learning.
Matthieu Dufour, Université du Québec à Montréal
Title: New results on circular NIM
Abstract: Matthieu Dufour and Silvia Heubach have been studying Circular Nim, a variation on the well-known game of NIM. This t:wo player game, described with two parameters and noted C(n,k), is played in the following way: n stacks of tokens are arranged in a circular way, and a move consists of choosing k consecutive stacks of this circular arrangement and then taking at least one token from one or more of the k stacks. In normal play, C(n,1), C(n,n-1) and C(n,n) are trivial. C(4,2) is easy, C(5,2), C(5,3) and C(6,3) are known since (Ehrenborg and, Steingrimsson, 1996) and C(6,4) and C(8,6) were solved by Dufour and Heubach (2012). We will present some more results, conjectures and comments on the misere play of that game.

